Арифметическое n-мерное вектороное пространство
1) Арифметический n-мерный вектор: α 1; α 2; α 3;.....;α n - действительные числа(компоненты арифметического вектора). 2) Пусть   . .Тогда  . . . .  . . . .вектор, противоположный  . .вектору 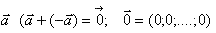 нулевой вектор. нулевой вектор. |
6)Линейная зависимость системы векторов. *) 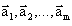 линейнозависимы⇔ линейнозависимы⇔ среди чисел k1,k2,...km есть хотя бы одно, отличное от нуля. *) если "длинная система" векторов линейно выражается через "короткую" систему векторов, то длинная система векторов линейно зависима. *) если система векторов  линейно зависима и линейно выражается через систему векторов  то m ≤ k. то m ≤ k.*) В арифметическом n-мерном вектороном пространстве любая система, содержащая более чем n векторов линейно, линейно зависима. |
3)  - арифметическое n-мерное векторное пространство -
это множество всех арифметических n-мерных векторов с операциями сложения арифметических векторов и умножение
арифметических векторов на действительные числа. - арифметическое n-мерное векторное пространство -
это множество всех арифметических n-мерных векторов с операциями сложения арифметических векторов и умножение
арифметических векторов на действительные числа.4)Скалярное произведение арифметических векторов.  норма (или длина арифметического вектора)    ортогональные векторы  5) Линейная комбинация векторов 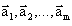 . . . .
|
Базис системы векторов *) S1 - базис системы S, если а) S1 - линейно зависима; б) всякий вектор S линейно выражается через векторы S1. *) Одним из базисов векторного пространства является система единичных векторов:  . .*) Любой базис векторного пространства состоит в точности из n векторов. *) Базис системы S арифметических n-мерных векторов содержит не более n векторов (т.е. от 1 до n векторов). *) Базис системы S составляет те векторы системы, номера которых совпадают с номерами главных неизвестных в общем решении вектороного уравнения:   - векторы системы S. - векторы системы S.*) ФНР - это базис подпространства решений. |